Probabilistic World

Mean and Variance of Probability Distributions

Posted on Written by 13 Comments

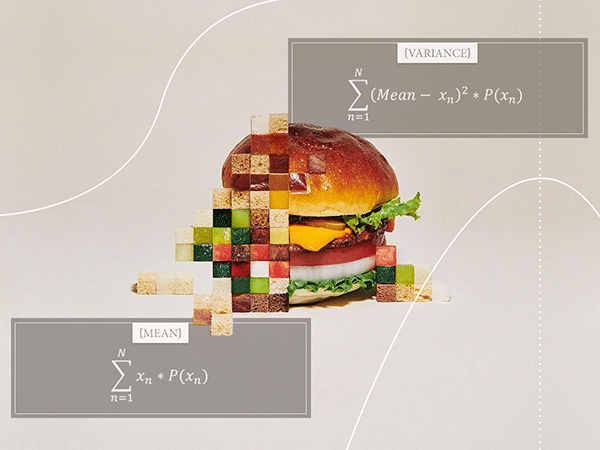
In my previous post I introduced you to probability distributions.

In short, a probability distribution is simply taking the whole probability mass of a random variable and distributing it across its possible outcomes. Since every random variable has a total probability mass equal to 1, this just means splitting the number 1 into parts and assigning each part to some element of the variable’s sample space (informally speaking).

In this post I want to dig a little deeper into probability distributions and explore some of their properties. Namely, I want to talk about the measures of central tendency (the mean) and dispersion (the variance) of a probability distribution.

[Read more…]

Introduction to Probability Distributions

Posted on Written by 7 Comments

If you want to take your understanding of probabilities to the next level, it’s crucial to be familiar with the concept of a probability distribution.

In short, a probability distribution is an assignment of probabilities or probability densities to all possible outcomes of a random variable.

For example, take the random process of flipping a regular coin. The outcome of each flip is a random variable with a probability distribution:

  • P(“Heads”) = 0.5
  • P(“Tails”) = 0.5

Depending on the type of random variable you’re working with, there are two general types of probability distributions: discrete and continuous. In this post, I’m going to give an overview of both kinds. And in follow-up posts I’m going to individually introduce specific frequently used probability distributions from each kind.

[Read more…]

Not All Zero Probabilities Are Created Equal

Posted on Written by 8 Comments

Im_possible

What does a probability of zero mean? When people use it in everyday conversations, a statement like “the probability of something is zero” usually implies that that something isn’t going to happen. Or that it is impossible to happen. Or that it will never happen.

There’s zero chance I’m passing this exam!

Is this true? Can we really say that zero probability events are impossible to occur? I’m going to show you that this is, in fact, false. You will see zero probability events are more than possible: they happen all the time.

[Read more…]