Cryptography During World War I

Welcome to part 5 of my series on cryptography! Today, the focus is going to be on codes and ciphers used during World War I. With a special focus on the most notable ciphers, as well as a particular code and the message it was used to encode. The latter — the Zimmermann Telegram — was a secret message whose interception had a dramatic effect on the dynamic of the war.

This post is part of my series Cryptography: Historical Intro & Combinatoric Analysis.

I’m going to start with a quick overview of how cryptography developed in the centuries prior to the war. Then, I’m going to give you a quick overview of the war itself and what contemporary cryptographic methods generally looked like at the time.

In the main part of the post, I’m going to focus on 4 of the most notable ciphers used during the war. Of course, as in all other posts from the series, we’re also going to perform a combinatoric analysis of each cipher and determine its overall security against brute-force attacks. If you’re new to this topic, check out my introductory post on combinatorics. I would also recommend checking out my post on the sum operator, since we’re going to use this notation for most analyses. Finally, I’m going to show you the most famous cryptographic code used to encode the most famous diplomatic blunder of all time.

Well, without further ado, let’s delve into today’s topic.

Cryptography before the 20th century

Since its birth and until the 20th, cryptography’s history was wild and messy. Its development had been driven by individuals (more or less independently), rather than by a collective effort. The process of collective learning, which had matured much earlier in other fields, only started happening when people began to realize cryptography’s true importance.

Well, recognizing cryptography’s importance is really about recognizing the power of information. It’s a somewhat unfortunate fact that war was the primary domain in which this recognition occurred but it does make sense, if you think about it. After all, by definition, war involves at least two mutual enemies who want to keep a lot of information secret from each other. On the other hand, some of the information needs to be shared among different structures within each party in the form of messages. And since the actual messages have always been prone to interception, making the intercepted messages unreadable is the natural solution.

Communication technologies themselves were also a major driving force for the development of more effective and reliable cryptographic methods. In the last post on cryptographic codes, I already told you about the major ways in which the electric telegraph changed communication dynamics in the 19th century. Making long-distance communications more effective naturally leads to a higher number of messages. And more messages means a higher risk of interception, hence a higher demand for cryptography.

Well, whatever the telegraph did to communication dynamics, it was still nothing compared to what radio communication did in the first half of the 20th century. But we’ll get to that in a bit.

Famous ciphers and codes

Let’s remember the big picture of cryptography:

• Ciphers
  • Transposition ciphers
  • Substitution ciphers
    • Monoalphabetic ciphers
    • Polyalphabetic ciphers
• Codes

Cryptographic methods fall under two major categories — codes and ciphers. Codes operate at the level of larger chunks of meaningful text (such as words), whereas ciphers typically operate at the level of individual characters and below. The latter fall under two subcategories — transposition and substitution ciphers. The former shuffle the characters, whereas the latter substitute them with other characters. Finally, substitution ciphers fall under two subcategories, depending on whether the substitution rule changes according to the characters’ position in the text — monoalphabetic and polyalphabetic ciphers.

Here is a list of the main codes and ciphers I’ve talked about in the series so far:

• Column cipher — one of the simplest (and oldest) transposition ciphers
• Caesar cipher — one of the simplest (and oldest) substitution ciphers

• Alberti’s cipher — one of the first polyalphabetic ciphers
• Trithemius’ cipher — another polyalphabetic cipher which became the basis of more advanced ciphers from this class
• Bellaso’s cipher — another polyalphabetic cipher that is closest to what we today call the Vigenère cipher
• Vigenère cipher — the most famous polyalphabetic cipher before the 20th century
• Autokey cipher — a more advanced (and secure) version of the Vigenère cipher
• One-time pad — the theoretically most secure cipher (in practice, very difficult to use)

• Alberti’s code — a simple cryptographic code implemented on the same device as Alberti’s cipher
• Mary’s nomenclator — a sophisticated (for its time) code/cipher hybrid
• Stager’s route cipher — a “cipher” which acts more like a code where words within the message are substituted and shuffled
• Baravelli’s code — a 19th century code using a proper codebook

If you’ve been following my series, by now you must have a pretty good understanding of how cryptography developed up until the 20th century. With all this background information, I’m ready to introduce you to 20th century cryptography. Particularly, I want to show you the role cryptography played during World War I.

But before that, to really get in the mood, let’s briefly talk about the war itself.

The Great War

World War I is the second largest military conflict in history, surpassed only by World War II. It started in the summer of 1914, after the assassination of the Austro-Hungarian heir Franz Ferdinand during his visit to the capital of the province of Bosnia and Herzegovina.

The war was fought between two camps — the Central Powers and the Allied Powers — and lasted until late 1918. The main participants on the side of the Central Powers were Germany, Austria-Hungary, the Ottoman Empire, and Bulgaria. On the side of the Allied Powers were France, Britain, Russia, and Italy. Many other countries joined the conflict at different stages (including the United States on the side of the Allied Powers).

The assassination of Franz Ferdinand was the main trigger for the war. However, the actual reasons were complex and had been building up since (at least) the 19th century.

Why did the war happen?

I already mentioned some of the tensions between France and Germany in the previous post of the series. When discussing the Dreyfus Affair, I told you about the Franco-Prussian war that preceded it (and France’s bitterness over lost territories). Germany itself had ambitions to play a much bigger role in the aggressive colonization of Africa that had recently started, where it was critically “lagging behind” France and the British Empire. The decline of the Ottoman Empire gave rise to a lot of internal tensions in many of its former (and soon-to-be former) territories in North Africa, the Middle East, and the Balkan Peninsula.

Speaking of the Balkans, the end of the 19th and the beginning of the 20th century were marked by many diplomatic and military conflicts between Bulgaria, Serbia, Romania, Greece, and the Ottoman Empire. In fact, in the last two years before the war, the region was shaken by the Balkan Wars which further destabilized it. On top of that, there was an intense competition between Austria-Hungary and Russia for territory and influence over the countries in that region.

As far as the reasons for the war go, I’m merely scratching the surface here. But, in short, the tensions between major powers were very high and the Balkans were the “perfect” place to light the match under those tensions.

Here’s a short video by OverSimplified which presents the beginning of the war in a fun way (you’ll find part 2 of the video below):

Long story short, the Central Powers lost. But let me give a short overview of the progress of the war. Of course, with more focus on the parts relevant to the ciphers and codes I want to show you afterwards.

Overview of WWI

Shortly after the assassination of Franz Ferdinand, Austria-Hungary declared war on Serbia. Then, one by one, the other participating countries went on to declare war on each other. Germany’s plan was to quickly knock France out of the war while Austria-Hungary was dealing with Serbia and Russia. Then, once France was out, they’d turn their focus to the East and help Austria-Hungary in achieving the ultimate victory. They decided to attack France from the north through Belgium but had to fight the “uncooperative” Belgium along the way. This drew Britain into the war, an event facilitated by Britain’s obligations coming from the Treaty of London guaranteeing Belgium’s neutrality.

The first few months established the war dynamic for the next four years. Germany’s plans for a quick victory in France failed, as did Austria-Hungary’s plans for a quick victory in Serbia. The conflict gradually turned into a big stalemate. Neither side was able deliver a decisive blow to the other, especially on the Western Front.

A large part of the war was marked by the so-called trench warfare. Armies faced each other in deep trenches. Furthermore, barbed wire, concrete, steel, and heavy artillery were some of the many new advanced defensive means that made breaking through enemy lines surprisingly difficult (and deadly!).

Progress of the war

In 1915, the war entered its main phase. Now, newer and deadlier weapons (like tanks and poison gas) were introduced. After more than a year of unsuccessful attempts to break the stalemate, in 1916 two of the deadliest battles in history took place — the Battle of Verdun and the Battle of the Somme. Together, those two battles alone claimed more than a million lives. In 1917, the US joined the war on the side of the Allied Powers, although their presence wasn’t truly felt until 1918.

By 1918, all major countries were exhausted… And that’s putting it mildly! The populations were starving, the armies’ morale was at an all-time low. Nobody had expected this conflict to last as long as it did. Early in that year, Russia became the first country to crack under the pressure and leave the war. This allowed Germany to shift their Eastern Front armies to the Western Front in a final attempt to crush the Allies. This was the so-called Spring Offensive. They needed to do so before the US had time to bring enough troops to Europe and tip the scales in favor of the Allies.

But, ultimately, this attempt also failed and, one by one, the Central Powers countries capitulated. First was Bulgaria in September, followed by the Ottoman Empire, Austria-Hungary, and finally Germany in November.

Oh, and here’s part 2 of the OverSimplified video I promised to share with you:

The naval blockades

Since the start of the war, Britain was employing a successful naval blockade over Germany. And this was draining Germany’s resources necessary to continue the war. On the other hand, Germany’s navy couldn’t match that of Britain and they were unable to end the blockade or initiate a successful counter-blockade.

However, Germans had another ace up their sleeve. Even though they couldn’t face Britain’s navy in an open battle, they used a strategy called unrestricted submarine warfare.

Using a type of submarines called U-boats, without warning, they were sinking any merchant ship trying to approach Britain’s shores. They had to temporarily stop this practice in 1915, out of fear of drawing the US into the war. This decision came after angry US reactions to the sinking of passenger ship RMS Lusitania on 7 May 1915 by a German U-boat. On that day, 1198 people died of which 128 were American citizens.

However, in late 1916, Germany realized they would run out of war resources (of almost any kind) faster than the Allies. So, they planned to begin using unrestricted submarine warfare again in the early months of 1917.

On the 1^st of February, they indeed resumed the campaign more aggressively than ever. And they were successful! Between February and April, U-boats sank more than 500 merchant ships. At some point, Britain was near starvation with only 6 weeks of food supplies left. After May, to reduce losses, the British admiralty adopted a widespread convoying of merchant ships (along with military escorts) which managed to significantly reduce losses. Still, by the end of the year, the Allies had lost 6,235,878 tons of merchant shipping to U-boat attacks. For comparison, in 1915 the losses were “only” 1,307,996 tons.

Keep all these events in mind, as they are quite relevant for the things we’re going to discuss in the main section.

Overview of cryptography during WWI

The invention of the electric telegraph increased the traffic of messages dramatically. This happened because you no longer needed to deliver messages through another living being. Messages could now travel through electric wires close to the speed of light. But the telegraph requires physical cables linking the communicating parties, which was still an inconvenience. And during war times, it can turn into a liability. For example, one of the first things Britain did at the start of the war was to destroy Germany’s cables in the Atlantic Ocean!

But what if communication didn’t need any special medium and could be sent through air? Well, this is exactly what became possible after one of the greatest inventions in human history — the radio! It was invented at the very end of the 19th century and World War I became the first big war in which it was used. Naturally, making communications more effective also increased communication traffic by several orders of magnitude. During the war, France alone intercepted messages consisting of more than 100 million words in total… From Germany alone!

Well, most of the messages had to be sent in secret. So, good cryptography was needed. Throughout World War I, the most advanced cryptographic methods of the time were put to use on all fronts. The type of methods fell roughly under two large categories, depending on the level of secrecy and urgency of the messages.

Standard codes

Most participating countries made wide use of the types of codes I showed you in the last part of the series. The most common uses were for naval, diplomatic, and strategic communication. In general, using codes is more cumbersome compared to ciphers, since the encoding/decoding process is significantly slower. Furthermore, the secure distribution of codebooks is always a challenging task, especially when the communicating parties are constantly on the move.

On the other hand, these codes were considered far more secure than ciphers. That’s why they were preferred for communication that required absolute secrecy. Of course, the codes themselves were improved too. Now the codebooks were richer in vocabulary and with more sophisticated superencipherment methods.

In the last section, I’m going to show you the most famous diplomatic code of the war (and perhaps of all time).

Trench codes and field ciphers

As their name suggests, armies used trench codes primarily in the trenches. Or, more generally, in active battlefields. These were less sophisticated codes with a much smaller vocabulary of up to only a few thousand words. Which made them less secure but easier to distribute.

The lower security wasn’t necessarily a serious issue. Even if the enemy managed to break the code for a particular message, it wouldn’t matter too much unless they break it fast enough. The situation on the battlefield is changing quickly and old information becomes useless very fast. Furthermore, even if a particular codebook is compromised, it’s much easier to replace it, compared to the large codebooks of the codes.

Still, trench codes had their limitations. Even a small codebook isn’t easy to replace when you have hundreds of units using them. That’s why field ciphers were a commonly preferred alternative. Not only because changing a cipher key is much easier, but also because using ciphers itself is much easier. And for military tactics efficiency is of paramount importance.

An good example of a field cipher was the German Übchi cipher. This was a double transposition column cipher (with shuffled columns) like the one I described in part 1. The French were quite good at breaking it, however, and Germans abandoned it early in the war. In the later stages, they used another (supposedly more secure) double transposition cipher they called ALACHI.

Austria-Hungary and Russia used some modified versions of the Vigenère cipher but they weren’t very secure for the standards of those days. The Italians also used a very similar polyalphabetic cipher with the name cifrario tascabile (meaning “pocket cipher”).

Notable field ciphers during WWI

Well, I hope I managed to get you in the right mood with this long introduction. Now I want to show you four of the famous field ciphers from the war. To make it easier to digest, I made a short video for each cipher illustrating the process of encipherment with dummy messages.

Of course, as in the rest of the series, we’re going to look at the combinatoric complexity of each.

Playfair (British)

The Playfair cipher was known and used even before World War I. As with all field ciphers, the British used it for tactical communication. Later on, the Americans picked it up too when they joined the war.

This cipher falls strictly under the category of polyalphabetic substitution ciphers and is quite easy to implement. Here’s how it works.

First, you need a previously agreed upon secret key. I’m going use the key “Probabilistic World” for this illustration. Once you have the key, you enter its letters into a 5×5 matrix in the same order, skipping duplicate letters. Here’s how we’d do it with our key:

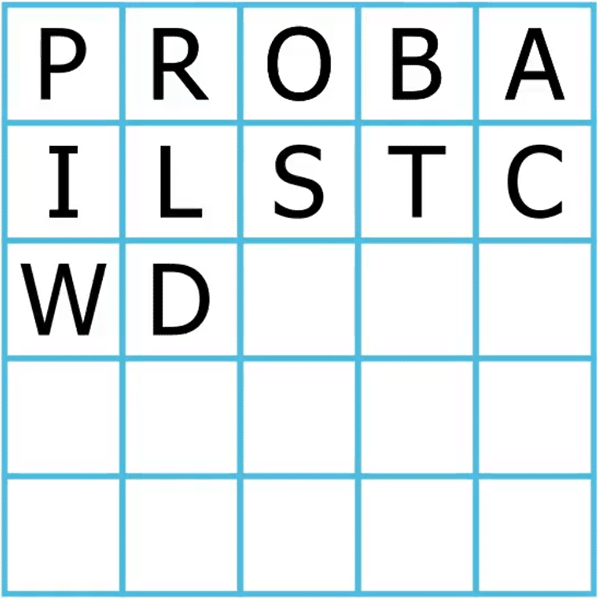
Next, you fill the remaining empty cells in the matrix with the letters from the alphabet in their natural order. Again, skipping any letters that are already in the key:

Since the Latin alphabet has 26 letters, we omit the letter J and replace it with I (if J appears anywhere in the plaintext).

Now, once we have the matrix, we’re ready to encipher. Let’s say we want to send the message “We are surrounded! Send more supplies!”. The first step is to break the message into pairs of letters (digrams). If the number of letters is odd (as is the case here), you append a null character to the end to complete the last digram. Most commonly, this null was the letter X (or Q):

WE AR ES UR RO UN DE DS EN DM OR ES UP PL IE SX

Also, if any of the digrams consists of two copies of the same letter (which we don’t have here), we replace the second with a null.

Then, one by one you, you substitute the letters of each digram according to the positions of the letters in the key matrix. Here’s how.

How encipherment works

For each digram, you identify the positions of the two letters in the matrix and apply the following substitution rules:

1. Same row: substitute each letter with the one to its right.
2. Same column: substitute each letter with the one below it.
3. Different row and different column: substitute each letter with the one on the same row but the column of the other letter.

For rules 1 and 2, if the letter is the last in its row or column, you “wrap around” and substitute it with the leftmost or topmost letter in the respective row/column instead. For rule 3, you basically pick the letters of the opposite corners of the imaginary rectangle the two letters form. Here’s an illustration for each rule.

The letters of the first digram (“WE”) happen to be on the same row, which means we should substitute each with the letter to its right. Therefore, we encipher “WE” as “DF”:

The letters of the third digram (“ES”) are in the same column, so we substitute each letter with the one below it. So, “ES” becomes “ME”.

The sixth digram has the letters “UN”, which fall on different rows and columns and form the following rectangle:

We substitute each letter with the one on the opposite corner, hence “UN” becomes “YH”.

Finally, let me also show you an example of rule 2 where one of the letters is on the edge. The letters of the thirteenth digram (“UP”) fall in the same column:

Here U is the last letter in the column, so we “wrap around” the column and replace it with the first letter P. And we replace the second letter P in the usual way with the one below it. So, “UP” becomes “PI”.

The final ciphertext

Here’s a short video which shows how we encipher the entire message from start to finish:

So, with the key “Probabilistic World”, the message “We are surrounded! Send more supplies!” becomes:

DFPOMEVPOBYHEFELFMEKBOMEPIRISWEO

Combinatoric analysis

Apart from the fancy way in which we generate the key matrix, at the end of the day it all boils down to determining the order of the letters in it.

Since we can’t make any assumptions about the keyword (and its length), we can’t a priori rule out any specific matrix. Which means that, as potential eavesdroppers, we need to test all possible matrices. Well, if we were trying to break the cipher with brute-force methods anyway.

Because there are 25 positions and 25 different letters in the matrix, the number of possible key matrices is simply equal to the number of permutations of 25 items. Which is simply equal to 25! (25 factorial) and so the number of possible keys here is:

   

Notice that, as far as brute-force solutions are concerned, this cipher is essentially equivalent to the simple substitution cipher I showed you in this section of part 1 of the series. The only difference is that here we have 25 positions, instead of 26. But that doesn’t really have a great effect on the security score.

Brute-force security score: 7

Interrupted columnar transposition (French)

The French used the interrupted columnar transposition cipher for very similar purposes to the British’s use of the Playfair cipher (tactical communication on the battlefield). As its name suggests, this is a transposition cipher.

This cipher is almost identical to the traditional column cipher with shuffled columns. You again enter the plaintext into a matrix whose number of columns is equal to the length of the keyword. And the keyword letters determine the order in which you transpose the columns to form the ciphertext. Because there often are duplicate letters, it’s easier to put a number next to each letter that represents its alphabetic rank. For example, with the key “we live in a probabilistic world”, the column labels look like this:

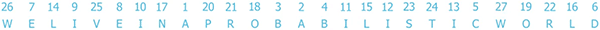
Notice that, for duplicate letters, their rank additionally depends on their position in the key. For example, there are two A’s, so the leftmost gets assigned 1 and the next gets assigned 2.

But there’s an additional enciphering feature. Prior to going through the columns, you go over prespecified right and left diagonals. Their letters become the first letters of the ciphertext. The choice of diagonals is also part of the key, along with the keyword that determines the column number and order. For example, we could specify columns 3, 5, 7, 8, and 17 to be the onsets of the right diagonals and columns 16, 18, 21, and 23 for the left diagonals. Let’s mark those with red and green, respectively:

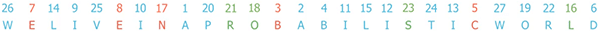
To see how it works, let’s consider an actual example.

How encipherment works

Say we want to encipher the text:

“We are surrounded by enemy forces! We need fifty calibre machine gun ammunition, send more supplies immediately! If you can, try to make a diversion from the north.”

And let’s write it out as a matrix:

Notice that the last three entries are nulls in the form of the first letters of the alphabet (A, B, and C). That’ because, with this cipher, you need a completely filled matrix.

So, first we start with the right diagonals, in ascending order. For example, the first right diagonal starts at column 3:

Therefore, the first letters of the ciphertext become “DANOT…”. Then, you continue by writing the remaining right diagonals and afterwards all the left diagonals (again, in ascending order). For example, the first left diagonal starts at column 16 and reads “CNPYR”. Once you do the diagonals, you continue with column 1 (“RITTS”), 2 (“EAEFR”), and so on all the way to the last column.

But, importantly, if any letter has already been included at a previous step, you skip it if you go over it more than once. For example, the letters from the first right diagonal (starting at column 3) won’t appear again when you’re going through columns 3, 2, 4, 11, and 15.

Anyway, here’s another short video which shows how the entire message is enciphered from start to finish (there’s a lot of small text and you’ll probably want to see it in full screen):

And the final ciphertext is:

DANOTYHPOBEEMEVSDITIRIILNCNYRNTRUFTAENRMORSEE FRCSIFDLYCUREGEACWNIEEUDRNMDUNIBIDMEOCHMASTOA AMAYBUEIMFYNYOITHOEOORLAERAEEMENNEEMIWSUSKFPT

Combinatoric analysis

Remember the combinatoric complexity of the column cipher with shuffled columns? Here’s the formula we derived in part 2 of the series:

   

Here N is the length of the ciphertext and the index k runs through the possible key lengths. And, for each k, we’re adding the possible permutations, in order to account for all possible column orders.

But here the key has two additional elements: the right and left diagonals, which are specified independently. To see how they contribute to the complexity, let’s first assign the variables r and l to stand for the number of right and left diagonals (respectively). And, for a moment, let’s assume we know what their values are. If we also know the key length (k), in how many ways can we distribute the right and left diagonals across the k available positions?

Those of you who read my post on combinatorics will likely recognize that this is a job for the multinomial coefficient:

   

As a quick reminder, you use the multinomial coefficient to count the number of ways in which you can arrange N elements into several groups of different sizes. Well, in our case, we need to figure out the number of ways in which we can distribute k columns into three groups of sizes:

• r
• l
• k – r – l

The last group simply represents the regular vertical columns. Then, for each k we have:

   

And because each of these can be independently combined with any of the k! permutations, the number of keys formula becomes:

   

   

Notice that, to keep it simple, I omitted the lower and upper bounds of the sum. And we’re still assuming we know the values of r and l. If we didn’t, we’d have to do a triple sum, with two additional sums for the two values. But I want to show you that the number of keys is huge even when we know their values.

For example, say we know that and . Furthermore, assume we somehow know the key length is always between 20 and 50 characters long (the French tended to use long keys with this cipher). With these assumptions, we have:

   

Obviously, even with these unrealistic assumptions, the complexity of this cipher is orders of magnitude bigger than that of the Playfair cipher.

Brute-force security score: 9

Turning grilles (German)

Now let’s look at a cipher used by the Central Powers. In particular, by Germany, albeit for only a few months at the end of 1916 (since it turned out it wasn’t the most secure of ciphers).

The Grille cipher (also known as turning grilles) is a pure transposition cipher that uses a square made up of smaller squares. Crucially, there were holes at the positions of a quarter of the smaller squares. For example, you could have a 6×6 square consisting of 36 squares, 9 of which are missing:

The particular pattern of 9 missing squares is the key for this cipher.

The Germans used squares of different sizes, depending on the length of the message they wanted to send (like 7×7 or 10×10), always removing a quarter of the small squares. If their total number is not divisible by 4, they simply used the quotient of the Euclidean division by 4 and filled the unfilled positions after the 4 90-degree turns with the remaining letters.

How encipherment works

The encipherment process is very simple. You start writing the letters of the plaintext in the empty squares from top to bottom and from left to right. That is, you enter it across the rows of the square, skipping any square that’s not empty.

For example, let’s encipher “We are surrounded! Send more supplies!” again. We can enter the first 9 letters of this plaintext like so:

Once you fill all the empty squares, you rotate the big square by 90 degrees and enter the next 9 letters of the plaintext into the empty squares. Then you repeat the procedure two more times and remove the big square. What you’re left with is the plaintext entered along the rows of a 6×6 matrix but in a different order. Finally, you create the ciphertext by joining the rows of this matrix.

Let me just show you another short video which should make the whole procedure very clear:

And the final ciphertext becomes:

DWOULIMEAENDROERDEESSXUSXXSUPRENXXPR

Notice that we appended five nulls in the form of the letter ‘X’ to the end, in order to make it exactly 36 characters long. On the other hand, if the plaintext were longer than 36 letters, we would simply encipher the first 36 letters and then return the big square to its starting position and continue enciphering the rest.

Combinatoric analysis

So, here there’s two things we need to know:

1. The size of the square
2. The pattern of missing squares

For 1, we can assume we know it ranges from 5×5 to 10×10, which means it consists of 25, 36, 49, 64, 81, or 100 small squares.

For 2, we know that of the squares will be empty. Which means that we just need the binomial coefficient, right? For example, for a 6×6 square we have possible patterns… Well, not so fast!

You see, not all of those patterns work. For every 90-degree rotation of the square, the small squares need to land on positions they haven’t landed on so far! Therefore, with every choice of a square, you’re eliminating 3 other squares — the positions corresponding to where the square lands after each turn.

This means that for the first square we have 36 available options. For the second, we have options. For the third we have options. And so on, until we’ve selected all 9 squares. Using the rule of product, this means the number of possibilities is simply the product of these numbers:

   

   

To express this product compactly, we can use the following mathematical notation, called the product operator:

   

Basically, this notation is identical to the sum operator, with addition replaced by multiplication. Now we can express the above product compactly as:

   

Notice that, to select exactly 9 squares, the upper bound is 8, instead of 9, because the index starts from 0.

Now, let’s generalize this expression for an arbitrary nxn square:

   

The notation means the quotient of the Euclidean division of x by y (in case is not divisible by 4). Again, notice we’re subtracting 1 because the index starts from 0.

Finally, we need to sum over the possible values of n, which we know range from 5 to 10:

   

I realize this is the first time I’m using some of this notation, so if you find any part confusing, feel free to ask a question in the comment section below.

Anyway, that’s a pretty high number, so attacking this cipher with pure brute-force approaches is quite fruitless.

Brute-force security score: 9

ADFGX and ADFGVX (German)

The last field cipher I want to show you today is a mixture between a substitution and a transposition cipher. Germany introduced it in early 1918 and used it for communications between divisions, corps, and army headquarters during the Spring Offensive I told you about earlier. After extremely hard work, the French eventually succeeded in breaking this cipher, which was of great help in achieving some crucial tactical victories over Germany.

The cipher’s name initially was ADFGX and shortly after it became ADFGVX (after a small modification). I’m going to focus mainly on the description of ADFGX because the ADFGVX modification doesn’t change the nature of the cipher.

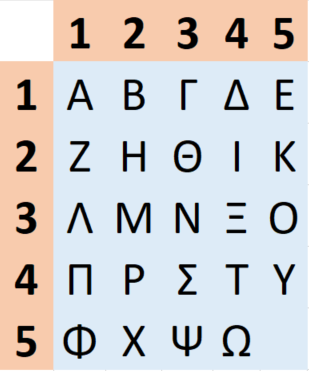
So, the key for this cipher consists of 2 parts – one keyword for substitution and one for transposition. You construct the substitution key matrix in an identical manner as that for the Playfair cipher we already covered. You enter the letters of the keyword into a 5×5 square, skipping duplicates and completing with the remaining letters from the Latin alphabet (again, replacing J with I). The only difference is that the rows and columns are labeled with the letters ADFGX.

For example, the keyword “Probabilistic World” creates the following matrix:

The way to use this square is by replacing every letter from the plaintext with two letters corresponding to that letter’s row and column labels, respectively. For example, the letter P would become AA, the letter K would become GD, and so on. This produces an intermediate ciphertext which is exactly twice as long as the plaintext.

Then, as the second step, you pass the intermediate ciphertext through one or two rounds of columnar transposition. For which you use the second keyword to construct the matrix (number of columns and their order). And that’s it!

How encipherment works

Take a look at the final short video that illustrates the application of this cipher with the two keywords “Probabilistic World” and “PWORLD” (for the first and second rounds of encipherment, respectively). This time, let’s use it to encipher the short message “We are surrounded!”, with a single round of columnar transposition:

As you can see, the final ciphertext becomes:

XFDGDADAGFFFAXFFAXAFFFDAFADAFD

If there were a second round of transposition, all you’d have to do is pass this ciphertext through the second step of the procedure again.

Shortly after the Germans introduced ADFGX, they modified it to the more secure ADFGVX. Which simply meant making the first matrix 6×6, with row/column labels ADFGVX. The 11 new available slots were filled with the letter J and the digits 0 through 9. Which means ADFGVX could support enciphering numbers directly, instead of having to verbalize them first. Other than that, it’s operation was identical to ADFGX.

Combinatoric analysis

Each of the two keys has an identical complexity as two ciphers’ keys we’ve already looked at.

Constructing the key for the substitution step is basically equivalent to that of the Playfair cipher and has a complexity of 25! or 26!. Depending, of course, on whether you’re using ADFGX or ADFGVX.

And the second key is equivalent to that of the column cipher with shuffled columns, which we know is . Here N is the length of the intermediate ciphertext and the index k represents the keyword length.

Because each possible candidate for the first key could be combined with every candidate for the second, the total number of possible key combinations is:

   

This is another simple application of the rule of product.

This formula will produce huge numbers even for moderately large N, which renders this cipher quite secure. In fact, not just towards brute-force attacks. Georges Painvin, one of the famous (and brilliant) French cryptanalysts of the time, did manage to learn to break this cipher after months of extremely hard work. Work so stressful that it brought him physical and mental illnesses from which he had to recover for months.

Brute-force security score: 9

The infamous Zimmermann Telegram

Alright, after getting a sense of the types of field ciphers WWI armies used, it’s time to move one level up, to diplomatic communication with codes. Before I show you the actual code, however, let me give you some more important historical context for it.

So, you remember in 1915 Germany had promised to stop unrestricted submarine warfare but then in 1916 changed its mind and wanted to start again, right? Well, one of the obvious problems with this decision was that it was likely to draw the US into the war. Something Germany really didn’t want! They were already struggling tremendously and the last thing they needed was a new powerful enemy with fresh forces.

In an attempt to partially neutralize this prospect, the German Foreign Secretary Arthur Zimmermann sent a secret message to the German ambassador in Mexico in which he proposed an alliance between the two countries.

In fact, let me show you the original telegram’s draft:

And here’s the English translation:

Basically, Germany was promising to help Mexico take back US territories lost in the 19th century! In return, Germany was asking Mexico to attack the US, in order to split their forces. Of course, only in the event that the US joins the war in Europe.

Well, such a daring proposition would no doubt outrage Americans, if they found out about it. Therefore, it was extremely important to send the message secretly.

German diplomatic code 13040

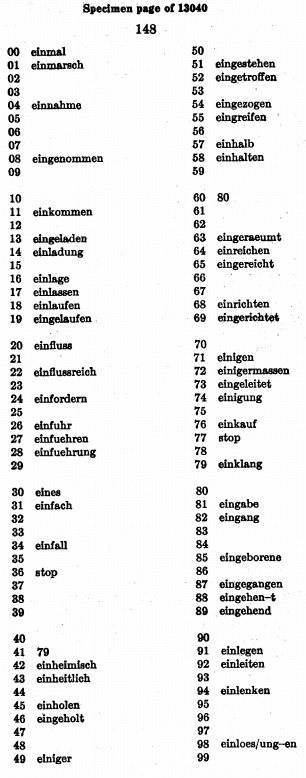
Germans used diplomatic code 0075 to send the Zimmermann Telegram to the German embassy in the US. From there, it was forwarded to the German embassy in Mexico using diplomatic code 13040.

On the right, you see a page from a partial reconstruction of the codebook for this code. I took this image from a 1937 declassified document from NSA’s online library. The actual 13040 codebook consisted of more than 20 thousand entries (19200 of which in the main vocabulary), arranged in 5 categories — the main vocabulary, grammatical directions, a list of proper and geographic names, a list of common phrases, and a trinumeral code for numbering and dating messages.

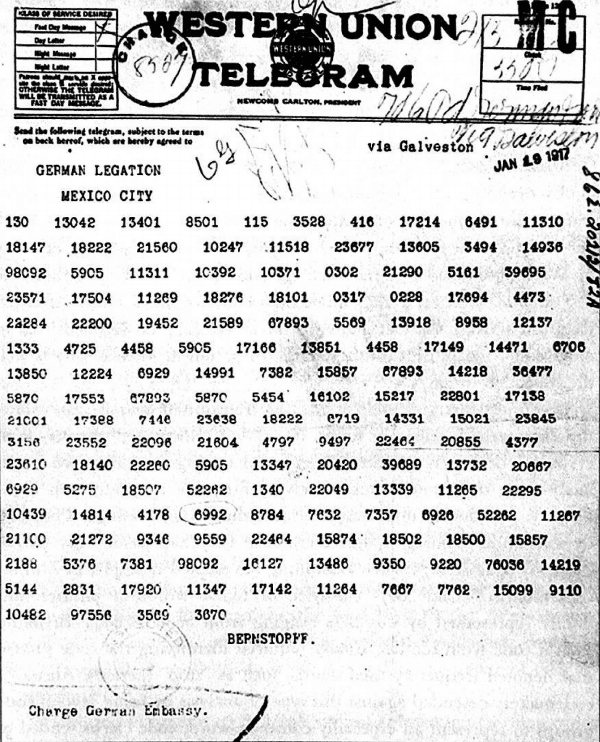
Lucky for us, we also have a preserved copy of the Western Union telegram sent from Washington to Mexico:

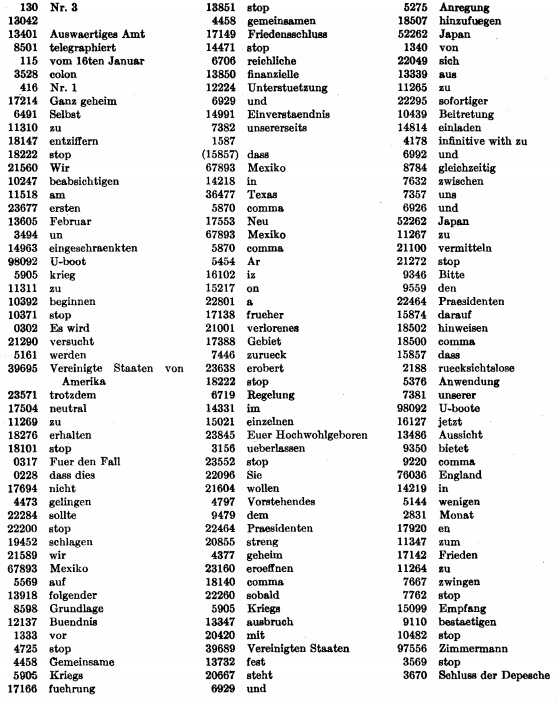
Here’s the meaning of each code block, taken from the а British reconstruction of the 13040 codebook:

Combinatoric analysis

The main vocabulary of code 13040 has 19200 words. So, according to the pattern we derived in the previous part of the series, the total number of possible codebooks here is:

   

Yes, this is an unbelievably large number! It’s an integer with almost 74 thousand digits. Most calculators won’t even be able to deal with this factorial. To give you some perspective, the total number of atoms in the universe is an extremely tiny fraction of this!

So, all the time and resources in the world won’t even come close to being enough to try out all possible codebooks for code 13040. And here we’re not even considering the remaining 4 parts of the code besides the main vocabulary. Code 13040 is practically unbreakable with a brute-force approach.

Brute-force security score: 10

Breaking the code and its consequences

Well, as it happened, despite its resistance to brute-force attacks, the code was not unbreakable by other means. Let me tell you what happened.

Since Britain is an island nation, a successful naval blockade would drain their resources faster than anything. So, Germans thought that a few months of unrestricted submarine attacks on merchant ships would force Britain to seek peace. And they also thought that, even if the US did enter the war, it wouldn’t happen soon enough to successfully intervene.

And the Germans were justified in their reasoning. At the time, there was a strong anti-war sentiment in the US. After all, just 2 months earlier, the American president Woodrow Wilson had won his re-election with the slogan ‘‘He kept us out of war’’.

Now, in the event that the US did enter the war, if they were then attacked by Mexico, that would distract them and delay their aid to the Allies for even longer. At least, that was Zimmermann’s reasoning. However, things didn’t quite go as planned. As it happened, the British intercepted and broke the code of the telegram. And that changed everything.

Earlier I showed you the original draft of the Zimmermann telegram. Let’s take a look at the text of the final version of the message that was delivered to the German embassy in Mexico (as decrypted and translated by British intelligence):

The telegram itself was most likely going to be inconsequential, since Mexico wasn’t really in a position to attack the US. What was consequential, however, was its decryption.

The United States of America enters WWI

Two days after Germany’s declaration of unrestricted submarine warfare, Woodrow Wilson broke off all diplomatic relations between the two countries. But there was still strong internal resistance towards joining the war among the population.

Two weeks earlier, British intelligence had intercepted and partially decrypted the Zimmermann Telegram. But it wasn’t until the 24^th of February when this actually reached Wilson. The entire story behind breaking the code and presenting its contents to the US is very interesting by itself. If you’re curious, you can read more details about it and the people involved in this awesome blog post.

Anyway, after Wilson saw the telegram, he was naturally outraged. A week later, the telegram was also known to the US Congress and was published all across US newspapers. Now, everybody in the US was outraged!

And this was the final straw that helped convince the American public that the US should join in the effort to defeat Germany.

One can only speculate how much longer the US would have hesitated to enter the war without the Zimmermann Telegram. But, as it happened, the Congress declared war on Germany just a month later, on the 6^th of April 1917. And this, eventually, completely ruined Germany’s hopes for success in the war, since they didn’t expect a US entry for at least a few months after their declaration of unrestricted submarine warfare.

Could the 1918 German Spring Offensive have been successful without the powerful military boost the Allies got from the US entry into the war? The answer to this question is actually surprisingly difficult. Many historians think the Central Powers did have a decent chance at prevailing, had the US not entered. Especially after Russia left the war in early 1918.

Well, for better or worse, things happened the way they did. But I’m sure these events let you appreciate the significance of the role cryptography (and cryptanalysis) played during the war.

Summary

I hope today’s post managed to give you a good sense of what cryptography looked like during World War I. And, crucially, the extremely important role cryptography played during the war at all levels. Which only solidifies the overall role of cryptography on the scene of world history, albeit mostly behind the curtains… A topic we’ve gone through extensively in this series so far.

So, overall we explored four of the famous field ciphers used during WWI:

• Playfair cipher, used by the British and the Americans (substitution cipher)
• Interrupted columnar transposition cipher, used by the French (transposition cipher)
• Turning grilles cipher, used by the Germans (transposition cipher)
• ADFGX and ADFGVX, used by the Germans (substitution/transposition cipher hybrid)

And I also showed you the German diplomatic code 13040, which was one of the codes used for enciphering the notorious Zimmermann Telegram that indirectly contributed to the early entry of the US into WWI.

You might have noticed that all these methods were largely based on simpler methods that have their roots in early history. Two of the four field ciphers (interrupted columns and ADFG(V)X) were based on the column cipher, which is one of the earliest cryptographic ideas in human history. Also, two of the four ciphers (Playfair and ADFG(V)X) were based on the so-called Polybus square, which is another early method I talked about all the way back in part 2 of the series dedicated to ancient cryptography.

Which, at least in my mind, speaks to the elegant brilliance of these simple ideas. Even though they lacked almost any security, with small modifications, they became the building blocks of powerful techniques that got employed 2000 years after their original invention!

Anyway, this is it for today. I hope you benefitted from this post and, as always, leave any feedback in the comment section below!

Oh, and here’s a summary of the combinatoric analysis for the methods we looked at today.

Brute-force security scores

Let’s take a final look at the methods I showed you today, each with its brute-force security score and the formula for calculating it.

• Playfair
  • Number of keys formula: 
  • Brute-force security score: 7
• Interrupted columnar transposition
  • Number of keys formula: 
  • Brute-force security score: 9
• Turning grilles
  • Number of keys formula: 
  • Brute-force security score: 9
• ADFGX
  • Number of keys formula: 
  • Brute-force security score: 9
• Code 13040
  • Number of keys formula:
  • Brute-force security score: 10