
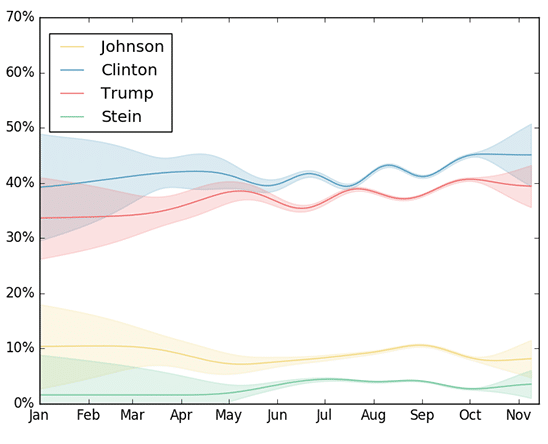
This is an update to the main post from September 20. Please click on the link for a detailed description of the election process and how we model it to make the predictions you see below. Click here to go back to the daily predictions page.
You can click on the date above the map to check the predictions for other dates. You can also click on different states on the map to see our state-specific predictions.


 Combinatorics is a branch of mathematics with applications in fields like physics, economics, computer programming, and many others. In particular, probability theory is one of the fields that makes heavy use of combinatorics in a wide variety of contexts.
Combinatorics is a branch of mathematics with applications in fields like physics, economics, computer programming, and many others. In particular, probability theory is one of the fields that makes heavy use of combinatorics in a wide variety of contexts. You can think of probabilities as
You can think of probabilities as